


Theme
OSCE and Standard Setting
Category
OSCE
INSTITUTION
Radboud University Medical Centre

Given that reliability, homogeneity and validity of OSCE’s can be improved at the expense of each other, the improvement process of OSCE's is complex, laborious and in need of extensive information. MSA provides a broad selection of parameters and analyses that could contribute to this process.
The use and interpretation of classical item analyses are not unchallenged in determining homogeneity and reliability in Likert scale checklists1,2,3.
It may be argued that item analysis based on nonparametric item response theory (NIRT) adds value to interpreting homogeneity and reliability in Objective Structural Clinical Exams (OSCE’s).
A sample of three OSCE checklists, comprising physical examination, history taking and communication was analyzed with the NIRT method of Mokken Scale Analysis (MSA)4.
For every checklist fit with the Monotone Homogeneity Model (MHM) and the Double Monotone Model (DMM) was determined. Reliability was estimated with MSA coefficient Rho and coefficient Cronbach’s alpha.
Within each checklist, the MSA search procedure was used to identify possible subscales that fitted the MHM and DMM.
MSA is a promising method to supplement or substitute classical item analysis in investigating Likert type checklists of OSCE’s.
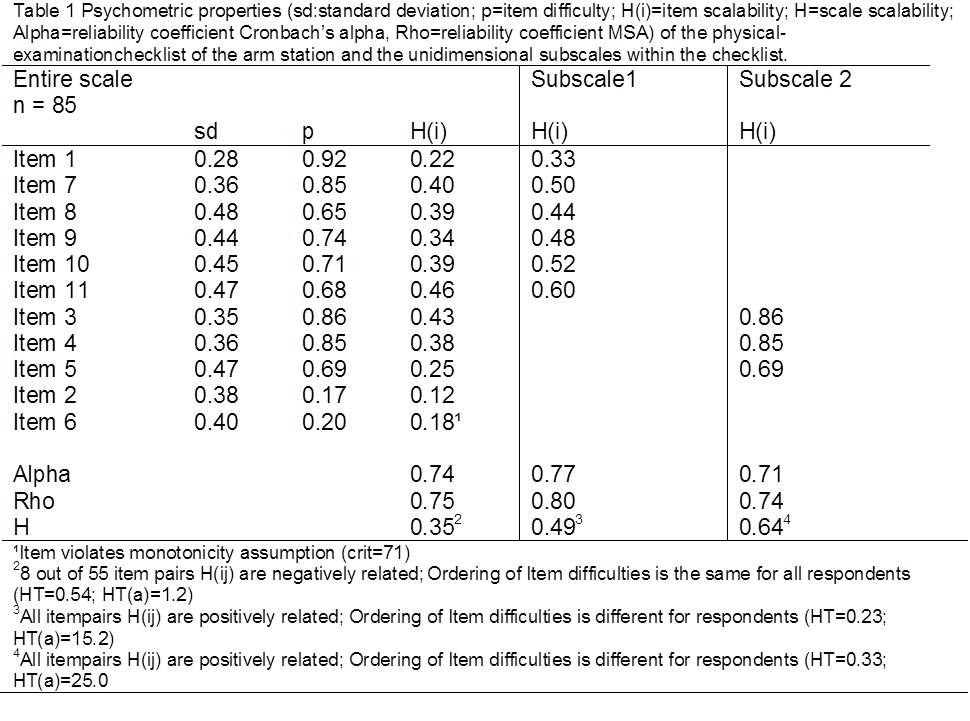
None of the three checklists fitted the MHM and the DMM. Reliability was sufficient for the physical examination checklist and the communication checklist but insufficient for the history taking checklist.
MSA´s search procedure revealed two subscales in the physical examination checklist that fitted the MHM. The history taking checklist comprised two subscales that fitted the MHM, one of which fitted the DMM as well. The communication checklist comprised three subscales that fitted the MHM, two of which fitted the DMM as well.
Reliability was sufficient for subscales comprising six items or more. Smaller subscales had insufficient reliability most of the time.
1Schuwirth, L. W. T., & van der Vleuten, C. P. M. (2006). A plea for new psychometric models in educational assessment. Medical Education, 40(4), 296-300. doi: DOI 10.1111/j.1365-2929.2006.02405.x
2Sijtsma, K. (2009a). On the Use, the Misuse, and the Very Limited Usefulness of Cronbach's Alpha. Psychometrika, 74(1), 107-120. doi: 10.1007/s11336-008-9101-0
3Sijtsma, K., & Emons, W. H. M. (2011). Advice on total-score reliability issues in psychosomatic measurement. Journal of Psychosomatic Research, 70(6), 565-572.
4Molenaar, I. W., & Sijtsma, K. (2000a). USER's Manual MSP5 FOR WINDOWS (Version 5.0 ed.). Groningen: iec ProGAMMA.
 Send Email
Send Email